TYBMS SEM 6 Operation Research (Q.P. April 2023 with Solution)

  Paper/ Subject Code 86001/ Operation Research

 TYBMS SEM 6

 Operation Research 

(Q.P. April 2023 with Solution)

1) April 2019 Q.P. with Solution (PDF) 

2) November 2019 Q.P. with Solution (PDF)

3) November 2022 Q.P. with Solution (PDF)

4) April 2023 Q.P. with Solution (PDF)

****************************************

Please check whether you have got the right question paper.

Note:

1. All questions are compulsory. (Subject to Internal Choice)

2. Figures to the right indicate full marks

3. Use of non-programmable calculator is allowed and mobile phones are not allowed.

4. Normal distribution table is printed on the last page for reference. Support your answers with diagrams / illustrations, wherever necessary

6. Graph papers will be supplied on request.

_________________________________________________

Q.1 A) State whether following statements True or False:(Attempt any8)         (8)

Video Solution Q.1 (a/b)  

1) Operation research is also termed as management science.

Ans: True

2) The objective function is a linear relationship reflecting the objective of an operation.

Ans:  False

3) The feasible region is a convex set.

Ans: True

4) the value of ∆j = Cj -- Zj row in the simplex table tells us whether the current solution is optimal, and, if it is not, what variable will be in the optimal solution.

Ans: False

5) if the assignment elements are cost elements,  then the objective of the optimal assignment is to maximize the cost. 

Ans: False

6) MODI method is the best method to get initials feasible transportation solution.

Ans: True

7) the dummy activity has an expected time of zero by definition. 

Ans: True

8 ) the PERT pessimistic time estimate is an estimate is an estimate of the minimum time an activity will require. 

Ans: True

9) in solving a job sequencing problem, it is assumed that all jobs require the same sequencing of operations.

ANS: False

10) if saddle point is available in a game, it is called as pure strategy game.             

Ans: True

Q.1B) Match the right and closely related answer from Column Y with the text / term given in Column X. ( Attempt Any 7 questions )

Column X	Column Y
1) Leaner relationship of Variable	a) Completely utilized resources
2) Infeasible region	b) Minimum cost in the table
3) Scarce resource	c) No feasible solution Possible
4) LCM	d) LPP
5) NWCR	e) In the game, gains of the winner are equal to total losses of all other players
6) Critical Activity	f) Optimistic time
7) Zero sum game	g) Fair game
8) Shortest activity time in PERT	h) Zero float value
9) Value of game =0	i) The time during which a machine is waiting or not working
10) Ideal time	j) Top left side corner of the side

 

Ans: 

Column X	Column Y
1) Leaner relationship of Variable	d) LPP
2) Infeasible region	c) No feasible solution Possible
3) Scarce resource	a) Completely utilized resources
4) LCM	b) Minimum cost in the table
5) NWCR	j) Top left side corner of the side
6) Critical Activity	f) Optimistic time
7) Zero sum game	e) In the game, gains of the winner are equal to total losses of all other players
8) Shortest activity time in PERT	h) Zero float value
9) Value of game =0	g) Fair game
10) Ideal time	i) The time during which a machine is waiting or not working

Q.2 A) M/S. Rajaram Pvt.ltd. and engineering firm has to decide profitable mix for its products i.e. Condenser, Transmitter and Connector with a profit (per 100 units) of 10, 16 and 4 respectively. To produce a shipment of condenser containing 100units required 1 hour of engineering 10 hours of direct labour and 2 hours of administration service. To produce one shipment of transmitter 1000 units require 1 hour of engineering 5 hours of direct labour and 6 hours of administration, similarly these figures for connectors are 1,4 and 2. There are 100 hours of engineering services available 600 hours of direct labour and 300 hours of administration. What is the most profitable mix find with the help of LPP formulation and simplex method.

From the above information Formulate as LPP

Solution:  

Material	Condenser	Transmitter	Conductor	Availability
Engineering	1	1	1	100
Direct labour	10	5	4	600
Administration service	2	6	2	300
Required	100	1000	1000

 Video Solution Q.2(a/b)

Let X₁ : No. of unit of condenser produce

X₂ : No. of unit of Transmitter produce

X₃ : No. of unit of Conductor produce

Max Z: Profitable of material produce

Max Z: 10 X₁ + 16 X₂ + 4 X₃

Subject Constraints:

            X₁ + X₂ + X₃ ≤ 100      --- [Engineering hours]

            10 X₁ + 5 X₂ + 4 X₃ ≤ 600 ---- [Direct labour hour]

            2 X₁ + 6 X₂ + 2 X₃ ≤ 300 --- [Administration service hours]

            X_{1 ,} X_{2 ,} X₃ ≥ 0

B) Find the optimum solution with the help of simplex method. 

Solution:  

Material	Condenser	Transmitter	Conductor	Availability
Engineering	1	1	1	100
Direct labour	10	5	4	600
Administration service	2	6	2	300
Required	100	1000	1000

 

Let X₁ : No. of unit of condenser produce

X₂ : No. of unit of Transmitter produce

X₃ : No. of unit of Conductor produce

Max Z: Profitable of material produce

Max Z: 10 X₁ + 16 X₂ + 4 X₃

Subject Constraints:

            X₁ + X₂ + X₃ ≤ 100      --- [Engineering hours]

            10 X₁ + 5 X₂ + 4 X₃ ≤ 600 ---- [Direct labour hour]

            2 X₁ + 6 X₂ + 2 X₃ ≤ 300 --- [Administration service hours]

            X_{1 ,} X_{2 ,} X₃ ≥ 0

Standard Form:

Max Z: 10 X₁ + 16 X₂ + 4 X₃ 

Subject Constraints:

            X₁ + X₂ + X₃ ≤ 100      --- [Engineering hours]

            10 X₁ + 5 X₂ + 4 X₃ ≤ 600 ---- [Direct labour hour]

            2 X₁ + 6 X₂ + 2 X₃ ≤ 300 --- [Administration service hours]

            X_{1 ,} X_{2 ,} X₃ ≥ 0

OR 

Q.2 C) Five salesmen are to be assigned to five territories. Based on past performance, the following table shows the annual sales (is Rs. lakh) that can be generated by each salesman in each territory. Find optimum assignment to maximize sales (MU. April 2015)

Video Solution Q.2(c/d)

Salesman	Territory
	T1	T2	T3	T4	T5
S1	26	14	10	12	9
S2	31	27	30	14	16
S3	15	18	16	25	30
S4	17	12	21	30	25
S5	20	19	25	16	10

Solution:

1) Regret Matrix (Converting to Minimization)

Salesman	Territory
	T1	T2	T3	T4	T5
S1	5	17	21	19	22
S2	0	4	1	17	15
S3	16	13	15	6	1
S4	14	19	10	1	6
S5	11	12	6	15	21

2) Row Minimization;

Salesman	Territory
	T1	T2	T3	T4	T5
S1	0	12	16	14	17
S2	0	4	1	17	15
S3	15	12	14	5	0
S4	13	18	9	0	5
S5	5	6	0	9	15

3) Column Minimization:

Salesman	Territory
	T1	T2	T3	T4	T5
S1	0	12	16	14	17
S2	0	4	1	17	15
S3	15	12	14	5	0
S4	13	18	9	0	5
S5	5	6	0	9	15

4) Analysis of Column Minimization

Salesman	Territory
	T1	T2	T3	T4	T5
S1	0	12	16	14	17
S2	0	4	1	17	15
S3	15	12	14	5	0
S4	13	18	9	0	5
S5	5	6	0	9	15

Min No. of Lines =5

Matrix size = 5x5

Therefore, Optimal Solution

5) Assignment:

Salesman	Territory
	T1	T2	T3	T4	T5
S1	0	12	16	14	17
S2	0	0	1	17	15
S3	15	12	14	5	0
S4	13	18	9	0	5
S5	5	6	0	9	15

6) Assignment Schedule;

Salesmen	Territory	Sales (Rs. Lacs)
S1 S2 S3 S4 S5	T1 T2 T3 T4 T5	26 27 30 30 25

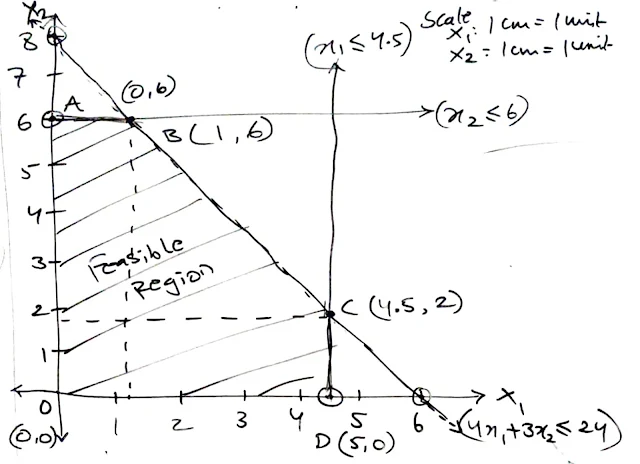
Optimal Sales = Rs. 138 Lacs

Q.2 D) Solve by using Graphical Method

Max Z = 4x₁ + 3x₂,

Subject to constraints:

4x₁ + 3x₂ < 24

x₁ < 4.5

x₂ < 6

x₁ , x₂ > 0

Q.3 A) From the data given below:

1. Draw a diagram                                                                                        (2)

2. Find Critical Path                                                                                     (2)

3. Crash Systematically the activities any determine optimal project duration: (4)

Activities	1-2	1-2	2-4	2-5	3-4	4-5
Normal time	8	4	2	10	5	3
Normal cost	100	150	50	100	100	80
Crash time	6	2	1	5	1	1
Crashed cost	200	350	90	400	200	100

Indirect cost is Rs. 70 per day

Video Solution Q. 3(a/b)

Q.3 B) You are given a solution for a transportation cost problem. Figures in each cell represent per unit transportation cost. Figures in circle within each cell represent number of units allocated for transportation. p_{1} .p 2 and P3 are the 3 Plants and W1, W2 and W3 are the3 Warehouses. You are required to check the above solution for optimality, if it is not optimal, use MODI method to obtain optimal solution and Find optimal transportation cost

Q.3C ) Project which is planned using PERT technique has following details of Average Expected Times calculated using the formula, te = (a + 4m + b) / 6 and the details of standard deviation.

Activities	Average Expected Time in weeks (te)	Standard deviation
1-2	3	4/6
1-3	4	4/6
2-5	5	4/6
2-4	6	2/6
5-6	7	4/6
4-6	8	4/6
3-6	9	4/6
6-7	3	2/6

i) Construct the network diagram of PERT network and find expected completion time of the project.                                                                                                            (3)

ii) Calculate the Variance of each activity.                                                            (4)

ill) Determine the probability of completing the project in 21 Weeks.                 (4)

iv) If the project manager wants to be 99% certain that the project should be completed on schedule what will be the project duration?                                                        (4)

Video Solution:

Solution: 

Q.4 A) You are given the pay-off (profit in 3) matrix in respect of a two person zero-sum game as follows:                                                                                                 (7)

1. Find the Maximin strategy. 
2. Find the Minimax strategy. 
3. What is the Value of the game.

Ans:

Video Solution

Q.4 B) Six jobs I, II, III, IV, V and VI are to be processed on two machine A and B in order AB

Jobs	Processing Time (Min.)
	Machine  A	Machine B
I	5	8
II	2	6
III	10	3
Iv	9	4
V	6	3
VI	8	9

(i) Find the sequence that minimizes the total elapsed time required to complete the jobs. (2)
(ii) Calculate the total elapsed time.                (3)
(iii) Idle time on for each Machine.                  (3)

OR

Q.4 C) Find the optimal sequence:                                        (8)

Jobs	I	II	III	IV	V
Machine  A	3	8	7	5	2
Machine  B	3	4	2	1	5
Machine  C	5	8	10	7	6

a) Determine the optimum sequence for performing jobs
b) Total minimum elapsed time
c) Idle time for each machine.

Video Solution;

Solution:

Q4 (D) you are given the following pay-off matrix of a zero-sum game, determine optimal strategies for the players and the value of the game.                                    (7)

A Strategy	B Strategy
	B1	B2	B3	B4
A1	5	-4	5	9
A2	6	2	0	-3
A3	9	15	10	11
A4	2	8	-6	5

Solution:  

Applied Principles of Dominances.

Row A3 dominates Row A1, A2 & A4 (As for A1, A2 & A4 all elements are less than Corresponding element of A3)

After Deleting we get:          B1     B2,     B3     B4

                                       A3 [  9        15        10    11 ]

Column B1 dominates column B2 B3 & B4.

After Deleting we get:           B1

                                        A3 [ 9 ]

Optimal Strategy A = A3

Optimal Strategy B = B1

Value of Game V*    = 9

Q.5 A) Define Operations Research. Explain limitation of Operation Research.

Ans:  Quantitative techniques can be classified in two groups, statistical techniques and programming techniques.

(A) Statistical techniques: Statistical techniques are applied in Statistics for data collection, data organization and data analysis. Some of the examples are:

(1) Mean, median and mode

(2) Mean deviation and standard deviation

(3) Probability theory

(4) Regression analysis and correlation analysis

(5) Sampling

(6) Statistical quality control

(B) Programming techniques: These are OR techniques. These techniques involve problem formulation, building mathematical models, substituting data in mathematical models, testing the model, using appropriate OR technique to solve the problem, obtaining optimal solution. Some examples are:

(1) Linear programming.

(2) Transportation problems.

(3) Assignment problems.

(4) Critical path method.

(5) Decision theory.

(6) Inventory management.

Some of the major limitations of OR techniques are:

(1) In construction of mathematical models, sometimes assumptions are necessary to simplify model construction. But over- simplification of a model or too many assumptions can make the model unrealistic.

(2) OR techniques are quantitative in nature. Hence, these techniques do not consider qualitative or intangible factors such as customer perceptions, employee motivation levels, quality of executives, advantage of experience etc.

(3) All business situations cannot be responded with quantitative techniques. Some business situations require gut feeling, initiative or managerial judgement. OR techniques cannot be applied in such situations.

B) Explain various cost involved in project crashing.

Ans: The execution of a project involves two types of costs, direct cost and indirect cost.

(a) Direct costs: These include costs of materials, machinery, tools, manhours etc. When we estimate the duration of various activities in the project, it is assumed that normal amount of labour (manhours) & machines will be required to complete these activities. The estimation of direct costs is done based on the normal amount of resource required. This estimation gives us minimum possible direct cost required to complete the project.

When we want to complete the project in a shorter period than critical path, we will need to employ more resources. Hence, direct cost will increase.

(b) Indirect costs: These include rent, overheads, administrative costs etc. Indirect costs vary with time. They are expressed on per day (or per week etc.) basis. Hence, when we shorten the project completion time, total indirect cost reduces.

(a) Normal time: The normal time is the activity duration under normal circumstances.

(b) Normal cost: The direct cost associated with the normal completion time. This is the minimum direct cost required for performing that activity.

(c) Crash time: The minimum possible time in which an activity can be completed.

(d) Crash cost: The direct cost associated with crash time of an activity. When an activity is crashed, its direct cost will increase.

Crash time < Normal time

Crash cost > Normal cost

The 'time-direct cost' relationship can be represented graphically like this:

OR

Q.5 C) Write a Short note (Attempt three):        (15)

i) Project crashing.

Ans:  In that case, the critical path will have to be shortened or reduced. This can be done by reducing completion time of some or all of the critical activities. To achieve this, we will need to employ extra resources. This process of shortening the critical path to achieve earlier completion of the project is called project crashing.

ii) Basis and non-basis variable in simplex table

Ans: (a) Basis variables: Basis variables in a simplex table mean those variables which are present in the basis of that simplex table. These are the variables which are in that particular solution.

(b) Non basis variables: Non basis variables in a simplex table mean the variables which are not in the basis of that simplex table. These are the variables which are not a part of that particular solution. In the test of optimality, we determine if it is possible to improve the solution by replacing one of the basis variables with one of the non- basis variables.

iii) Interfering float

Ans: Interfering float: It is that part of total float which reduces the float of a subsequent activity. It is the amount of time by which the earliest possible start of a subsequent activity will be delayed if activity ij finishes on latest finishing time.

Interfering float = Latest finishing time of activity ij - Earliest starting time of subsequent activity.

Interfering Float = Lj - Ej

iv) Objectives of critical path

The critical path method (CPM) is a project management technique used to identify the sequence of tasks that determine the minimum duration required to complete a project. The critical path represents the longest path through a project network diagram and determines the shortest possible project duration. The primary objectives of identifying and analyzing the critical path include:

1. Determining Project Duration: By identifying the critical path, project managers can determine the shortest possible duration required to complete the project. This information is crucial for planning and scheduling resources effectively.

2. Resource Allocation: Understanding the critical path helps in allocating resources efficiently. Tasks on the critical path cannot be delayed without extending the project's overall duration. Thus, it is essential to ensure that sufficient resources are allocated to critical tasks to prevent delays in the project timeline.

3. Task Prioritization: Tasks on the critical path are critical to the project's success. Therefore, they require special attention and priority in terms of monitoring, management, and resource allocation. By identifying the critical path, project managers can focus their efforts on managing these critical tasks to keep the project on track.

4. Risk Management: The critical path highlights tasks that are most susceptible to delays. By focusing on these critical tasks, project managers can proactively identify potential risks and develop strategies to mitigate them. This helps in minimizing the likelihood of delays and ensuring successful project completion.

5. Schedule Compression: Knowing the critical path allows project managers to identify opportunities for schedule compression. By focusing on critical tasks or adding resources to critical activities, project managers can accelerate the project timeline without affecting its overall duration.

v) NWCM

Ans: Northwest Corner Method (NWCM)

The Northwest Corner Method is a technique used in transportation and distribution problems to find an initial feasible solution. It is named as such because it begins by allocating as much as possible starting from the northwest corner of the transportation tableau.

Here's a brief overview of the Northwest Corner Method:

1. Initial Allocation: The method starts at the top-left (northwest corner) cell of the transportation tableau. It allocates as much as possible to satisfy the supply and demand constraints while minimizing transportation costs.

2. Move to the Next Cell: After allocating the maximum possible amount in the northwest corner cell, the method moves to the next cell along the same row or column. The process continues iteratively, moving either horizontally or vertically, until one of the supply or demand constraints is exhausted.

3. Iteration: The method iterates through the remaining cells, allocating quantities based on the remaining supply and demand constraints, always moving from the current allocation to the next available cell in the direction of the unfulfilled constraint.

4. Completing Allocation: The allocation process continues until all supply and demand requirements are met. At this point, the initial feasible solution is obtained.

5. Optimizing the Solution: While the Northwest Corner Method provides an initial feasible solution, it may not be optimal. Further optimization techniques such as the stepping stone method or the modified distribution method can be applied to improve the solution and minimize transportation costs.

The Northwest Corner Method provides a simple and straightforward approach to initially solving transportation and distribution problems. However, it may not always yield the most efficient solution, so additional optimization methods are often employed to refine the solution further.

Elective: Operation Research (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2022	November	Download	Solution
2023	April	Download	Solution
2023	November	Download	Solution
2024	April	Download	Solution
2024	November		Solution
2025	April

Elective: International Finance (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2022	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Brand Management (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April		Solution

Elective: HRM in Global Perspective (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Innovation Financial Service (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April		Solution

Elective: Retail Management (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download
2025	April

Elective: Organizational Development (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Project Management (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: International Marketing (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download
2025	April

Elective: HRM in Service Sector Management (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download
2025	April

Elective: Strategic Financial Management (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Media Planning (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Workforce Diversity (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download
2025	April

Elective: Financing Rural Development (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download
2025	April

Elective: Sport Marketing (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download
2025	April

Elective: HRM Accounting & Audit (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Indirect Tax (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Marketing of Non-Profit Organization (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April

Elective: Indian Ethos in Management (CBCGS)
Year	Month	Q.P.	Link
IMP Q.			Solution
Obj. Q			Solution
2019	April	Download	Solution
2019	November	Download	Solution
2023	April	Download	Solution
2024	April	Download	Solution
2024	November	Download	Solution
2025	April