Paper/ Subject Code 86001/ Operation Research
TYBMS SEM 6
Operation Research
(Q.P. November 2019 with Solution)
1) April 2019 Q.P. with Solution (PDF)
2) November 2019 Q.P. with Solution (PDF)
3) November 2022 Q.P. with Solution (PDF)
4) April 2023 Q.P. with Solution (PDF)
Please check whether you have got the right question paper.
Note:
1. All questions are compulsory. (Subject to Internal Choice)
2. Figures to the right indicate full marks
3. Use of non-programmable calculator is allowed and mobile phones are not allowed.
4. Normal distribution table is printed on the last page for reference. Support your answers with diagrams / illustrations, wherever necessary
6. Graph papers will be supplied on request.
___________________________________________
Q.1A) Match the right and closely related answer from Column Y with the text / term given in Column X. ( Attempt Any 7 questions )
|
Column X |
Column Y |
|
1) Value of Game = 0 |
a) Training programme scheduling |
|
2) Optimistic Time |
b) If no. of Row > No. of Columns |
|
3) Application of O.R. in HRM |
c) Minimization types transportation problem |
|
4) Pessimistic Time |
d) Does not affect the feasible solution |
|
5) Add Dummy Row in Assignment |
e) To maximize per capita income |
|
6) Redundant Constraint in Graphical |
f) one player’s gain is the other player’s Loss |
|
7) Application of O.R. in Finance |
g) If no. of Row < No. of Columns |
|
8) Transportation elements as time |
h) fair game |
|
9) Add Dummy Column in Assignement |
i) Shortest and ideal Time estimate in PERT |
|
10) Zero Sum Game |
j) Time estimate in PERT by considering worst delays |
ANS :
|
Column X |
Column Y |
|
1) Value of Game = 0 |
f) one player’s gain is the other player’s Loss |
|
2) Optimistic Time |
i) Shortest and ideal Time estimate in PERT |
|
3) Application of O.R. in HRM |
a) Training programme scheduling |
|
4) Pessimistic Time |
j) Time estimate in PERT by considering worst delays |
|
5) Add Dummy Row in Assignment |
g) If no. of Row < No. of Columns |
|
6) Redundant Constraint in Graphical |
d) Does not affect the feasible solution |
|
7) Application of O.R. in Finance |
e) To maximize per capita income |
|
8) Transportation elements as time |
c) Minimization types transportation problem |
|
9) Add Dummy Column in Assignement |
b) If no. of Row > No. of Columns |
|
10) Zero Sum Game |
h) fair game |
Q.1 B) State whether following statements
True or False: (Attempt any 8) (8)
1) One of the areas of application of Operations Research is in Agriculture.
Ans: False
2) A linear programming model consists of
only decision variables and constraints
Ans: True
3) In graphical method of LPP the optimum
value occurs anywhere in feasible region.
Ans: True
4) If the assignment elements are cost
elements then the objective of the optimal assignment is to maximize the cost.
Ans; False
5) In transportation problem, number of
basic allocated (or Occupied) cells should be exactly m+n+1, so that it becomes
non-degenerate.
Ans; False
6) Dummy activity does not consume time or
resources.
Ans: True
7) The three time estimates employed in
PERT are: optimistic time, average expected time, and pessimistic time.
Ans: True
8) In Sequencing the time taken by each job
in changing over from one machine to another is negligible.
Ans: False
9) The row [-1,10, 20] dominates the row [0,0,0]
Ans: False
10) The column [0,-1,-2] dominates the
column [0,-1, -1]
Ans: False
Q2 A) Use Graphical method to solve the following Linear programming problem (8)
Objective Function
Max Z = 3X1 + 4X2
Subject to Constraints
3X1 + 2X2 ≤ 18
X1 ≤ 5
X2 ≤ 6
X1 ,X2 ≥ 0
Ans:
Click here to Video Solution
3X1 +
2X2 ≤ 18 ---- (i)
3X1 +
2X2 = 18
Let X1 =
0
3(0) + 2
X2 = 18
2 X2 =
18 Therefore X2 =
9 (X1, X2)
= (0, 9)
Let X2 =
0
3 X1 + 2(0)
= 18
3X1 =
18 Therefore X1 =
6 (X1, X2)
= (6, 0)
X1 ≤ 5 ----
(ii)
Therefore X1
= 5 (X1, X2)
= (5, 0)
X2 ≤ 6 ----
(iii)
Therefore X2
= 6 (X1, X2)
= (0, 6)
Vertex Corner
Points :
|
Vertex |
Coordinate Points |
Max Z = 3X1
+ 4X2 |
|
O (0,0) |
X1 =
0, X2 = 0 |
3(0) + 4(0) = 0 |
|
A (0,6) |
X1 = 0, X2 = 6 |
3(0) + 4(6) = 24 |
|
B (2.5,6) |
X1 = 2.5, X2 = 6 |
3(2.5) + 4(6) = 31.5 |
|
C (5,2.5) |
X1 = 5, X2 = 2.5 |
3(5) + 4(2.5) = 25 |
|
D (5,0) |
X1 = 5, X2 = 0 |
3(5) + 4(0) = 15 |
Therefore Max Z =
31.5
where, X1 =
2.5, X2 = 6
Q2.B) There are 7 different products in a
machine shop. Their manufacturing time in Hrs on machines 1 and 2 are given
below. Each of the product must go through two machines and 2 in the order 1-2.
|
Products |
Time in HRs on Machine 1 |
Time in HRs on Machine 2 |
|
A |
20 |
10 |
|
B |
30 |
25 |
|
C |
10 |
25 |
|
D |
20 |
30 |
|
E |
55 |
35 |
|
F |
60 |
40 |
|
G |
50 |
45 |
i) Find the sequence of Products that
minimizes the total elapsed time.
(ii) Find the Total Elapsed Time for the
optimum Sequence.
(iii) Calculate the idle time for machine
1.
(iv) Calculate the idle time for machine 2.
Ans: i) The
sequence of Products that minimizes the total elapsed time
Machine 1 Machine
2
|
C |
D |
G |
F |
E |
B |
A |
|
Products |
Machine
1 |
Machine
2 |
||
|
In |
Out |
In |
Out |
|
|
C |
0 |
0 +
10 = 10 |
10 |
10 +
25 = 35 |
|
D |
10 |
10 + 20
= 30 |
35 |
35 +
30 = 65 |
|
G |
30 |
30 +
50 = 80 |
80 |
80 +
45 = 125 |
|
F |
80 |
80 +
60 = 140 |
140 |
140+
40 = 180 |
|
E |
140 |
140 +
55 = 195 |
195 |
195 +
35 = 230 |
|
B |
195 |
195 +
30 = 225 |
230 |
230+ 25
= 255 |
|
A |
225 |
225 +
20 = 245* |
255 |
255 +
10 = 265* |
Therefore, Total
Elapse Time for Machine = 265 Hrs
iii) Idle Time for
Machine :
Machine 1 = 265 –
245 = 20 Hrs
Machine 2 = 265 –
210 = 55 Hrs
OR
Q.2 C) 'BMS Ltd' prepared a set of
interdependent activities for their upcoming project; details of which is given
in below table
|
Activity |
Preceding Activity |
Duration (weeks) |
|
(1,2) A |
- |
2 |
|
(1,3) B |
- |
3 |
|
(2,4) C |
A |
3 |
|
(3,5) D |
B |
4 |
|
(4,6) E |
C |
3 |
|
(5,6) F |
C, D |
2 |
|
(6,7) G |
E. F |
9 |
|
(4,5)
Dummy |
C |
0 |
(i) Construct a network diagram, find
critical path and project completion time. (3)
(ii) Tabulate Calculate Earliest Start and
Finish Time, Latest Start and Finish Time and Total Float. (5)
Ans: Critical path :
A-C-G-E = 2 + 3+ 3+ 9 = 17 weeks
A-C-X-F-G = 2+3+0+ 2 + 9 = 16 weeks
B-D-F-G = 3 +4 + 2 + 9 = 18 weeks
Therefore, Critical path: B-D-F-G
Project Completion = 18 weeks
|
Activity |
EST =
Ei |
EFT =
Ei + t |
LST =
Lj + t |
LFT =
Lj |
|
(1,2)
A |
0 |
0 + 2
= 2 |
3 – 2
=1 |
3 |
|
(1,3)
B |
0 |
0 + 3
= 3 |
3 – 3
= 0 |
3 |
|
(2,4)
C |
2 |
2 + 3
= 5 |
6 – 3
= 3 |
6 |
|
(3,5)
D |
3 |
3 + 4
= 7 |
7 – 4
= 3 |
7 |
|
(4,6)
E |
5 |
5 + 3
= 8 |
9 – 3
= 6 |
9 |
|
(5,6)
F |
7 |
7 + 2
= 9 |
9 – 2
= 7 |
9 |
|
(6,7)
G |
9 |
9 + 9
= 18 |
18 – 9
= 9 |
18 |
|
(4,5)
Dummy |
5 |
5 + 0
= 5 |
7 – 0
= 7 |
7 |
Q.2 D) A company is transporting its units from three manufacturing plants P1, P2 and P3 to four distribution centres D1, D2, D3 and D4. The supply and demand of units with unit cost of transportation (in Rs.) and the schedule followed from plants to distribution centres are given below: (The numbers which are in circle indicates number of units transported from plant to distribution centre).
(i) Test the solution for optimality (3)
(ii) If solution is not optimal find
optimal solution. (4)
Q.3 A) Following payoff matrix refers to a two-player game, player and player B. Each player has four strategic options.
(i) Find the Maximin Strategy. (3)
(ii) Find the Minimax Strategy. (3)
(iii) What is the value of the Game? (1)
Q.3 B) There are five jobs (namely 1,2,3,4 and 5), each of which must go through machines A, B and C in the order ABC. Processing Time (in hours) are given below:
|
Jobs |
1 |
2 |
3 |
4 |
5 |
|
Machine A |
5 |
6 |
6 |
9 |
6 |
|
Machine B |
3 |
2 |
5 |
5 |
3 |
|
Machine C |
3 |
7 |
5 |
6 |
7 |
(i)Find the sequence
that minimizes the total elapsed time required to complete the jobs. (2)
(ii) Calculate
the total elapsed time (3)
(iii) Idle time
on Machine A, Machine B and Machine C. (3)
Ans: i) The
sequence of Products that minimizes the total elapsed time
Converting the 3-machines
problem into a fictitious 2-machines problem where G and H are the two fictitious
Machines.
G = A +
B
H = B +
C
|
Jobs |
1 |
2 |
3 |
4 |
5 |
|
Machine
G |
8 |
8 |
11 |
14 |
9 |
|
Machine
H |
6 |
9 |
10 |
11 |
10 |
Machine
G Machine
H
|
2 |
5 |
4 |
3 |
1 |
|
Jobs |
Machine
A |
Machine
B |
Machine
C |
|||
|
In |
Out |
In |
Out |
In |
Out |
|
|
2 |
0 |
0 + 6
= 6 |
6 |
6 + 2
= 8 |
8 |
8 + 7 = 15 |
|
5 |
6 |
6 + 6
= 12 |
12 |
12 + 3
= 15 |
15 |
15 +
7 = 22 |
|
4 |
12 |
12 +
9 = 21 |
21 |
21 + 5
= 26 |
26 |
26 + 6
= 32 |
|
3 |
21 |
21 +
6 = 27 |
27 |
27 +
5 = 32 |
32 |
32 +
5 = 37 |
|
1 |
27 |
27 +
5 = 32* |
32 |
32 +
3 = 35* |
37 |
37 +
3 = 40 |
iii) Idle Time for
Machine :
Machine A = 40 – 32
= 8 Hrs
Machine B = 40 – 18
= 22 Hrs
Machine C = 40 – 28
= 12 Hrs
OR
Q.3 C) Five
salesmen are to be assigned to five territories. Base on past performance, the
following table shows the annual sales (is Rs. lakh) that can be generated by
each salesman in each territory. Find optimum assignment to maximise sales.
|
Salesmen |
Territory |
||||
|
T1 |
T2 |
T3 |
T4 |
T5 |
|
|
S1 |
24 |
12 |
8 |
10 |
7 |
|
S2 |
29 |
25 |
28 |
12 |
14 |
|
S3 |
13 |
16 |
14 |
23 |
28 |
|
S4 |
15 |
10 |
19 |
28 |
23 |
|
S5 |
18 |
17 |
23 |
14 |
8 |
1)
Regret Matrix :
|
Salesmen |
Territory |
||||
|
T1 |
T2 |
T3 |
T4 |
T5 |
|
|
S1 |
5 |
17 |
21 |
19 |
22 |
|
S2 |
0 |
4 |
1 |
17 |
15 |
|
S3 |
16 |
13 |
15 |
6 |
1 |
|
S4 |
14 |
19 |
10 |
1 |
6 |
|
S5 |
11 |
12 |
6 |
15 |
21 |
2)
Row Minimization
|
Salesmen |
Territory |
||||
|
T1 |
T2 |
T3 |
T4 |
T5 |
|
|
S1 |
0 |
12 |
16 |
14 |
17 |
|
S2 |
0 |
4 |
1 |
17 |
15 |
|
S3 |
15 |
12 |
14 |
5 |
0 |
|
S4 |
13 |
18 |
9 |
0 |
5 |
|
S5 |
5 |
6 |
0 |
9 |
15 |
3)
Column Minimization / Analysis:
|
Salesmen |
Territory |
||||
|
T1 |
T2 |
T3 |
T4 |
T5 |
|
|
S1 |
0 |
8 |
16 |
14 |
17 |
|
S2 |
0 |
0 |
1 |
17 |
15 |
|
S3 |
15 |
8 |
14 |
5 |
0 |
|
S4 |
13 |
14 |
9 |
0 |
5 |
|
S5 |
5 |
2 |
0 |
9 |
15 |
3) Allocation:
|
Salesmen |
Territory |
|||||
|
T1 |
T2 |
T3 |
T4 |
T5 |
||
|
S1 |
|
8 |
16 |
14 |
17 |
|
|
S2 |
0 |
|
1 |
17 |
15 |
|
|
S3 |
15 |
8 |
14 |
5 |
|
|
|
S4 |
13 |
14 |
9 |
|
5 |
|
|
S5 |
5 |
2 |
|
9 |
15 |
|
4)
Calculating Total Sales:
|
Salesmen |
Territories |
Sales |
|
S1 |
T1 |
24 |
|
S2 |
T2 |
25 |
|
S3 |
T5 |
28 |
|
S4 |
T3 |
28 |
|
S5 |
T3 |
23 |
|
|
Total |
128 |
Q.3 D) Use
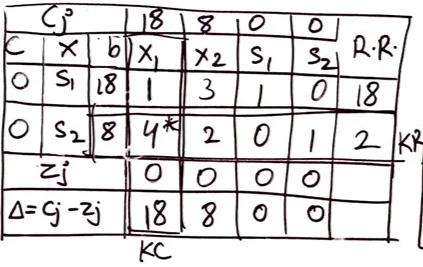
Simplex method to solve the following Linear programming problem (8)
Maximize Z=4x1+7x2
Subject to the
constraints.
x1+3x2
≤ 18
4x1
+2X2 ≤ 8
X1 ,
X2 ≥ 0
Maximize Z= 4x1+7x2
+ 0S1 + 0 S2
Subject to the constraints.
x1+3x2
+ 1S1 + 0 S2 ≤ 18
4x1 +2X2
+ 0S1 + 1S2 ≤ 8
X1 , X2,
S1, S2 ≥ 0
New Value of Key
Row = Old Value / Key Element
= 8 4 2 0 1
4
Corresponding
Key Row
= Old
Value – {Corresponding Value of Key Column – New Value of Key Row}
b = 18 –
(1 x 2) = 16
X1 = 1 –
(1 x 1) = 0
X2 = 3 –
(1 – 1/2) = 5/2
S1 = 1 –
(1 X 0) = 1
S2 = 0 –
(1 X 1/4) = -1/4
∆ is
Zero and Negative value.
It is
optimal solution.
Maximize Z=4x1+7x2
Where, X1 = 18 and
X2 = 0
Maximize Z= 4(18)+7(0)
= 72
Maximize Z= 72
Q.4 A) The table
given below has been taken from the solution procedure of a transportation problem,
involving minimization of cost (in Rs.)
i) Show that the
above solution is optimal. Find an optimal solution. (3)
ii) Does the
problem have multiple optimal solutions? Give reasons. (2)
iii) If multiple
solutions exist, then find one more optimal solution. (3)
iv) Comment upon
the managerial significance of multiple optimal solutions (2)
Allocation Cell : Cost = ui + vj {+, + = -} {+, - = +}
Since two optimal solution with Same minimum cost- are available must choose any one optimal Solution as per their convenience to the management- management
Q.4 B) A company
is making a chart to decide the minimum amount of constituents like proteins,
vitamins, carbohydrates, fats etc. Which a man needs on daily basis to fulfil
his requirement for medical awareness. The choice is to be made from different
type of foods (4 types). The yields per unit for different types of foods are
explained below in the chart. Formulate the given linear programming problem. (5)
|
Types of food |
Yield per Unit |
Cost per unit |
||
|
|
Proteins |
Fats |
Vitamins |
(Rs.) |
|
A |
5 |
6 |
12 |
130 |
|
B |
7 |
6 |
9 |
125 |
|
C |
16 |
20 |
14 |
160 |
|
D |
12 |
18 |
10 |
120 |
|
Minimum Req. |
1600 |
800 |
100 |
|
Ans:
Formulate LPP
Let X1 = No. of unit
of A
X2 = No. of unit
of B
X3 = No. of Unit
of C
X4 = No. of Unit
of D
Z = Total Cost
Min Z = 130 X1
+ 125 X2 + 160 X3 + 120 X4
Subject Constraints,
5 X1 +
7 X2 + 16 X3 + 12 X4 ≥ 1600 ------ (Proteins)
6 X1 + 6
X2 + 20 X3 + 18 X4 ≥ 800 ------ (Fats)
12 X1 +
9 X2 + 14 X3 + 10 X4 ≥ 1000 ------ (Proteins)
4) (C) A Project
which is planned using PERT technique has following details of Average Expected
Times calculated using the formula, te=(a+4m+b)/6 and the details of standard deviation
|
Activity |
Average Expected Time in weeks (te) |
S.D |
|
1-2 |
2 |
1 |
|
1-3 |
5 |
0.5 |
|
2-3 |
4 |
0.5 |
|
2-4 |
8 |
1 |
|
3-5 |
3 |
1 |
|
4-6 |
5 |
0.5 |
|
5-6 |
2 |
1 |
|
6-7 |
3 |
1 |
ii) Calculate
and tabulate the Variance of activity. (2)
b) iii)
Determine the probability of completing the project in 17 Weeks. (2)
iv) If there is
a huge penalty for exceeding the project completion deadline of two weeks after
estimated projected completion time (Tor Critical Path Duration). What is the
probability of being penalized? (2)
v) Find project
completion time for 95% confidence level. (2)
vi) If the fixed
cost of the project is Rs. 4000000/- and the variable cost is Rs. 20000/- per week.
Find the amount the firm should bid under the policy of 95% confidence of completion
of the project. (For the purpose of bidding, consider only cost that is break
even no loss and no profit) (2)
vii) If the
project manager wants to complete the project with 95% confidence in 19 weeks,
by how much time he crash the critical activities? (1)
viii) If the
head of activity 3-5 wants to work overtime so that he can complete this activity
in 2 weeks (instead of 3 weeks), should he be permitted? (1)
Ans:
|
Activity |
Average
Expected Time in weeks (te) |
S.D |
Variance
S.D2 |
|
1-2 |
2 |
1 |
1 |
|
1-3 |
5 |
0.5 |
0.25 |
|
2-3 |
4 |
0.5 |
0.25 |
|
2-4 |
8 |
1 |
1 |
|
3-5 |
3 |
1 |
1 |
|
4-6 |
5 |
0.5 |
0.25 |
|
5-6 |
2 |
1 |
1 |
|
6-7 |
3 |
1 |
1 |
1-2-4-6-7 =
2+8+5+3 = 18 weeks
1-2-3-5-6-7 = 2 +
4 + 3 + 2 + 3 = 14 Weeks
1-3-5-6-7 =
5+3+2+3 = 10 Weeks
Therefore,
Critical Path = 1-2-4-6-7
Project Completion
= 18 weeks
ii) Variance of
Critical Path = 1 + 1 + 0.25 + 1 = 3.25
S.D. = √3.25 = 1.8027
B) i) Time = 17
Weeks
Te = 17 weeks
Z = t – C.P. /
S.D.
Z = 17 – 18 / 1.80
Z = -1 / 1.80 = -
0.56
Table Value = -
0.2123
P (17 weeks) = 0.5
– 0.2123
=
0.2877
=
28.77 %
iv) Project
Completion = 18 + 2 = 20 Weeks
Penalty will
impose when project completion 20 Weeks.
P (Non-Completion)
= 1-p (20 Weeks)
Z = 20-18 / 1.80 = 2/ 1.80 =
1.11
Table Value =
0.3643
P(20 Weeks) = 0.5
+ 0.3643 = 0.8643
P (Non-Completion)
= 1- 0.8643
Penalty = 0.1357
Project completion time for 95% Confidence level
Confidence level = 95%
p = 0.95
Table value = 0.95 -0.5 = 0.45 (0.4505)
Corresponding Z = 1.65
Z = t - CP / S.D.
1.65 = t - 18 / 1.80
1.65 X 1.80 = t - 18
2.97 = t - 18
2.97 + 18 = t
t = 20.97 Appx 21 weeks
vi) If the fixed cost of the project is Rs. 4000000/- and the variable cost is Rs. 20000/- per week.
Total Cost = Fixed Cost + Variable Cost
= 40,00,000 + 20,000 (21) = 40,00,000 + 420,000 = 44,20,000
Project Manager should biding on Rs. 44,20,000 where he will get break even point.
vii) Since the corresponding project duration 95% confidence is 21 weeks, but the project manager wants to complete in 19 weeks.
Hence, Required Crashing = 21 -19 = 2 weeks
Viii) No, Project Manager should not allow to overtime the head activities 3-5.
Q.5 A) Define Operations Research. Discuss the advantages and limitations of O.R. (7)
Ans:
Definition of Operations Research:
One of the classical definitions of OR is - "Operations Research is the application of scientific methods, techniques and tools to problems involving the operations of systems so as to provide those in control of operations with optimum solutions to the problems."
LIMITATIONS OF OPERATIONS RESEARCH TECHNIQUES:
Some of the major limitations of OR techniques are: (1) In construction of mathematical models, sometimes assumptions are necessary to simplify model construction. But over- simplification of a model or too many assumptions can make the model unrealistic.
(2) OR techniques are quantitative in nature. Hence, these techniques do not consider qualitative or intangible factors such as customer perceptions, employee motivation levels, quality of executives, advantage of experience etc.
(3) All business situations cannot be responded with quantitative techniques. Some business situations require gut feeling, initiative or managerial judgement. OR techniques cannot be applied in such situations.
B) What do you mean by alternative optimal solution in an Assignment? How do you identify alternative solution in an Assignment problem? Further what is the procedure to find that alternative solution? (8)
Ans:
Alternate or Multiple Optimal Solutions:
An assignment problem can have more than one possible combination of Assignments it is a case of Alternate optimal solutions. But all possible combinations have the same final (optimal) answer.
An Assignment problem may have more than one optimal solution, which is called multiple optimal solutions. The meaning of multiple optimal solutions is - The total cost or total profit will remain same for different sets or combinations of allocations. It means we have the flexibility of assigning different allocations while still maintaining Minimum (Optimal) cost or Maximum (Optimal) profit.
We can detect multiple optimal solutions when there are multiple zeroes in any column or row in the final (Optimal) table in the Assignment problem. It means we have an option of allocating different assignments to a particular job or worker.
When the matrix fails the test for presence of optimal solution, we need to perform "iteration" to improve the solution (i.e. to remove degeneracy). In "iteration", we perform following operations for writing the next table:
[A] Find minimum uncovered value in the present matrix.
[B] Subtract it from all uncovered values in the matrix.
[C] Add it to all double covered values (i.e. intersection values) in the matrix.
[D] All other values in the matrix remain same.
OR
C) Answer Any
3 of the following: (15)
i) Assumptions in LPP
Ans: Assumptions in LP:
(1) Available quantities of resources and consumption per unit from resources is known exactly and with certainty.
(2) Production of finished products is possible in any fractions, so is consumption of resources.
(3) All external factors are constant.
(4) The problem involves only one major objective.
ii) Degeneracy in Transportation
Ans: DEGENERACY IN TRANSPORTATION:
Degeneracy occurs when in a Transportation table, number of allocations are less than [number of rows + number of columns - 1].
It means the rim condition is not satisfied.
Rim Condition:
Number of allocations should be equal to [m + n - 1] . Where,
m = Number of Rows.
n = Number of Columns.
If a transportation solution is degenerate, i.e., having degeneracy then we cannot calculate values of u and v'.
Hence, the solution cannot be tested for optimally (A cannot be calculated).
To remove degeneracy, we add an imaginary entry called Epsilon (e) in the solution.
Epsilon is a zero value allocation Its only purpose is to facilitate calculation of 'u and v'
Where to place Epsilon (e): Epsilon is placed in an independent position i.e., a position where it does not form a closed loop with other allocations.
This kind of looping between the allocations and Epsilon should not take place.
iii) Principles of Dominance
Ans: Principles of Dominance are used for reducing the game matrix of a two person zero-sum game, if the game matrix contains large number of strategies.
Principles:
(1) Rules for Rows: If All the elements in a Row are less than or equal to the corresponding elements in another Row, then this Row is said to be dominated by the another Row and can be eliminated from the game matrix to reduce the order of the matrix.
(2) Rules for Columns: If All the elements in a Column are greater than or equal to the corresponding elements in another Column, then this Column is said to be dominated by the another Column and can be eliminated from the game matrix to reduce the order of the matrix.
iv) Assumptions in Job Sequencing
Ans: PRINCIPAL ASSUMPTIONS:
(1) Each machine can perform only one type of operation and can undertake only one job at a time.
(2) Only one machine of each type is available.
(3) All jobs require the same sequence of operations.
(a) In a two machines problem, each job is processed first on machine A and then on machine B.
(b) In a three machine problem, the sequence of operations is A, B,C.
(4) The processing times of all jobs on all machines are known and remain constant.
(5) Each job must be completed before another job is taken up for processing.
(6) No job is required more urgently than the other.
(7) Transit time to move a job from one machine to another is negligible.
v) Dummy activity and its use in network analysis
Ans: DUMMY ACTIVITY:
A Dummy activity does not consume any time or resources. It is represented by a dotted line. The purpose of Dummy activity is to represent logical relationship of dependency.
Dummy activity is required in following cases: (a) Two activities are performed concurrently and a third activity depends on both of these activities.
(b) Two concurrent activities which need to be connected to correctly represent the precedence relationship of succeeding activities.
Elective: Operation Research (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| |
Obj. Q |
|
| |
2019 | April | ||
2019 | November | ||
2022 | November | ||
2023 | April | ||
2023 | November | ||
2024 | April | ||
2024 | November | ||
2025 | April |
|
|
Elective: International Finance (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| |
Obj. Q |
|
| |
2019 | April | ||
2019 | November | ||
2022 | November | Solution | |
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
|
|
Elective: Brand Management (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April | Solution | |
Elective: HRM in Global Perspective (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April | ||
Elective: Innovation Financial Service (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | Solution | |
2024 | April | ||
2024 | November | Solution | |
2025 | April | Solution | |
Elective: Retail Management (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | ||
2025 | April | ||
Elective: Organizational Development (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |
Elective: Project Management (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | Solution | |
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |
Elective: International Marketing (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | ||
2025 | April |
| |
Elective: HRM in Service Sector Management (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | ||
2025 | April |
| |
Elective: Strategic Financial Management (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |
Elective: Media Planning (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |
Elective: Workforce Diversity (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2023 | April | ||
2024 | April | ||
2024 | November | ||
2025 | April |
| |
Elective: Financing Rural Development (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2023 | April | ||
2024 | April | ||
2024 | November | ||
2025 | April |
| |
Elective: Sport Marketing (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2023 | April | ||
2024 | April | ||
2024 | November | ||
2025 | April |
| |
Elective: HRM Accounting & Audit (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |
Elective: Indirect Tax (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | Solution | |
2024 | November | Solution | |
2025 | April |
| |
Elective: Marketing of Non-Profit Organization (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| Solution |
Obj. Q |
|
| Solution |
2019 | April | Solution | |
2019 | November | Solution | |
2023 | April | Solution | |
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |
Elective: Indian Ethos in Management (CBCGS) | |||
Year | Month | Q.P. | Link |
IMP Q. |
|
| |
Obj. Q |
|
| |
2019 | April | ||
2019 | November | ||
2023 | April | ||
2024 | April | ||
2024 | November | Solution | |
2025 | April |
| |













.png)


0 Comments